📉 Tail Dependence – เมื่อเกิดวิกฤต ความสัมพันธ์เชิงเส้นล้มเหลว แล้วเราจะทำอย่างไร?

🎯 หากคุณเป็นหนึ่งในผู้ที่สามารถรอดพ้นจากความผันผวนของตลาดหุ้นสหรัฐฯ และสินทรัพย์ดิจิทัลในสัปดาห์ที่ผ่านมา — บทความนี้คือสิ่งที่คุณควรอ่านต่อ

บทความนี้นำเสนอแนวคิดเรื่อง Tail Dependence หรือ “ความสัมพันธ์ในหางของการแจกแจงร่วม” ซึ่งเป็นเครื่องมือสำคัญในเชิงสถิติและการวิเคราะห์ความเสี่ยงเชิงปริมาณ (Quantitative Risk Analysis)

📆 เหตุการณ์สำคัญในตลาดหุ้นสหรัฐฯ สัปดาห์ที่ผ่านมา

ในวันที่ 3 เมษายน 2025 ตลาดหุ้นสหรัฐฯ เผชิญกับความผันผวนอย่างรุนแรง:

ดัชนี S&P 500 ลดลงกว่า 4.84%
ดัชนี NASDAQ ลดลงกว่า 5.97%

ต่อมาในวันที่ 9 เมษายน 2025 ประธานาธิบดีโดนัลด์ ทรัมป์ได้ประกาศ ชะลอการขึ้นภาษีเพิ่มเติม (ยกเว้นกับจีน)
ส่งผลให้ตลาดพลิกกลับอย่างรุนแรง:

S&P 500 ฟื้นตัวขึ้น 9.5%
NASDAQ เพิ่มขึ้นถึง 12.2% ภายในวันเดียว

🔄 ความสัมพันธ์ของสินทรัพย์เปลี่ยนไปอย่างไร?

โดยทั่วไป นักลงทุนมักเข้าใจว่า:

หากสินทรัพย์สองรายการมีค่า Pearson Correlation ต่ำ พอร์ตการลงทุนจะมีความเสี่ยงรวมลดลง

อย่างไรก็ตาม เหตุการณ์ “Trump Tariff 2025” แสดงให้เห็นว่า
ความสัมพันธ์เชิงเส้น ที่วัดในช่วงปกติอาจ ล้มเหลว ในช่วงวิกฤต

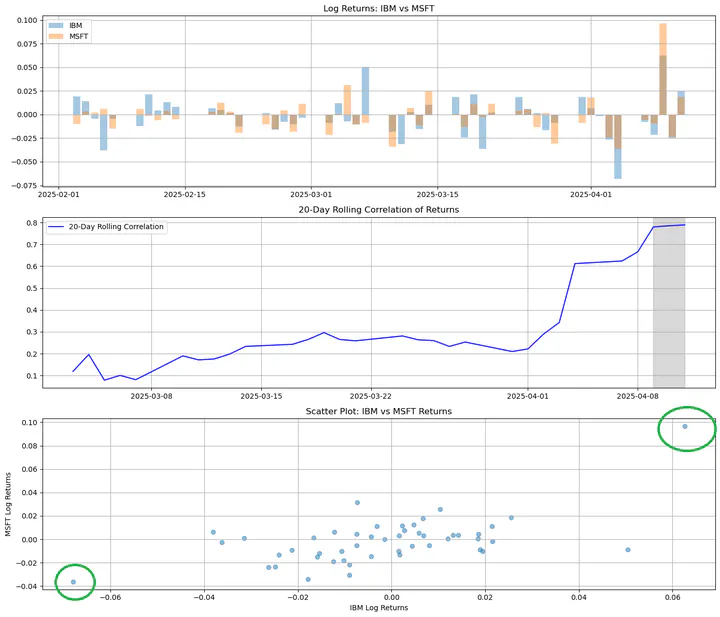
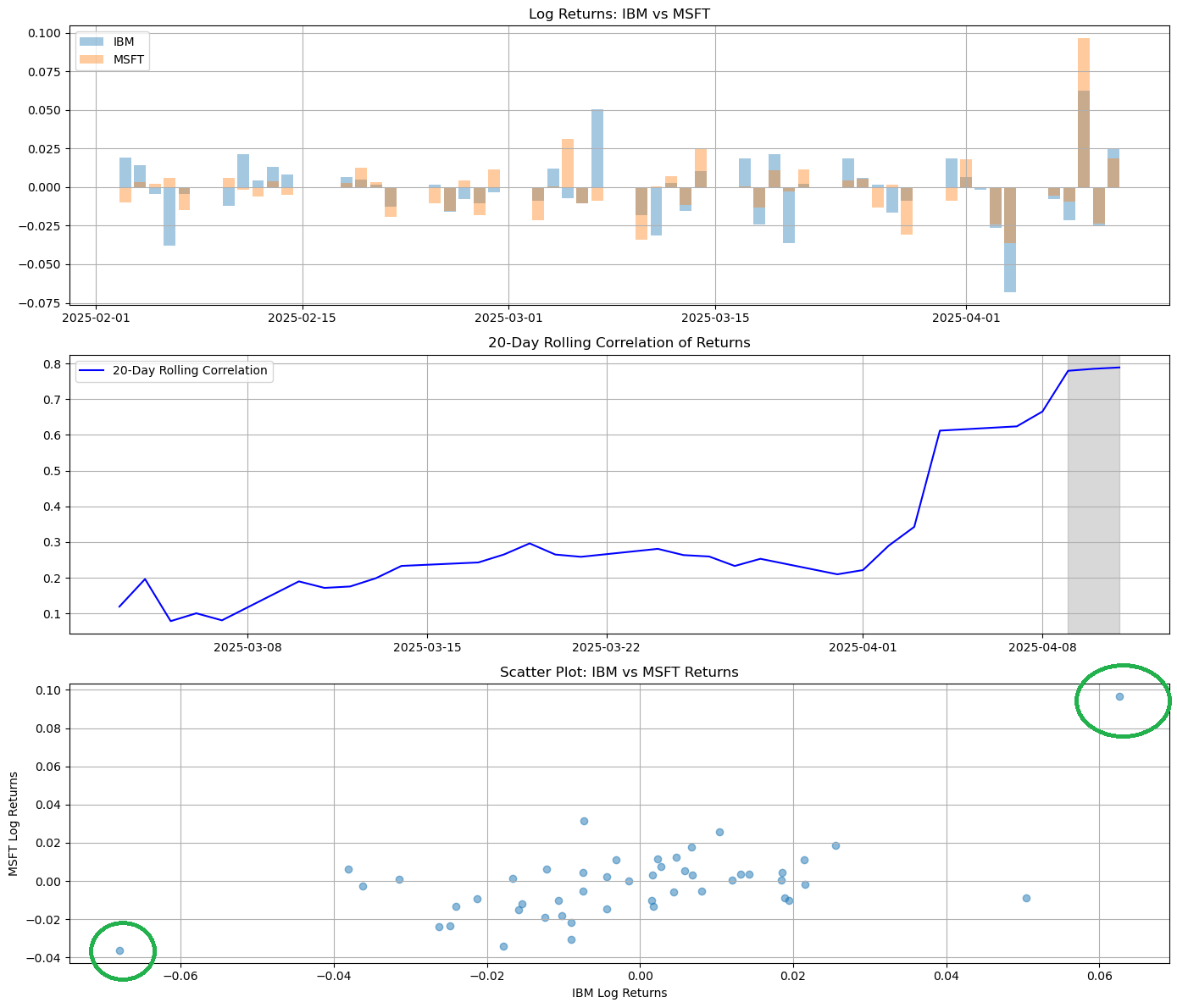
📌 ตัวอย่าง: จาก รูปที่ 1

ผลตอบแทนรายวันของ IBM และ MSFT โดยปกติมี Pearson correlation ~0.2
แต่ในช่วงเกิดเหตุการณ์ Tariff — ค่า correlation พุ่งขึ้นถึง 0.8
👉 สะท้อนว่าพอร์ตที่ดู “diversified” กลับประสบความเสียหายพร้อมกัน

##❗ นิยามของ Tail Dependence

ในโลกของ Math-Stat-Quant ความสัมพันธ์ไม่ได้จำกัดเพียง Pearson Correlation
เครื่องมืออื่น ๆ ที่ถูกใช้ได้แก่: Kendall’s Tau, Concordance, Directional Dependence และ Tail Dependence

Tail Dependence วัดว่า:

“เมื่อหนึ่งในตัวแปรร่วงหนัก (หรือพุ่งแรง) อีกตัวจะตามไปหรือไม่?”

เช่น หากตลาดหุ้นร่วงแรงในหางซ้ายของการแจกแจง Tail Dependence ช่วยวิเคราะห์ว่าสินทรัพย์อื่นจะมีแนวโน้มร่วงตามหรือไม่

ประเภทของ Tail Dependence:

Lower Tail Dependence: วัดโอกาสที่สินทรัพย์จะร่วงพร้อมกัน
Upper Tail Dependence: วัดโอกาสที่สินทรัพย์จะพุ่งแรงพร้อมกัน

🧪 ตัวอย่างจากข้อมูลจริง

ข้อมูลระหว่าง IBM และ MSFT สะท้อนลักษณะของ Tail Dependence อย่างชัดเจน

ในภาวะปกติ ค่า correlation อยู่ในระดับต่ำ (~0.2)
แต่ในช่วงที่ตลาดตกหนักและฟื้นตัวแรง ทั้งสองสินทรัพย์มีพฤติกรรมเหมือนกัน

📌 จาก รูปที่ 1 Panel 3:

ความถี่ของจุดใน มุมล่างซ้าย แสดงถึง Lower Tail Dependence
ความถี่ของจุดใน มุมขวาบน แสดงถึง Upper Tail Dependence

แม้ในช่วงกุมภาพันธ์–เมษายน 2025 จะมี Tail Dependence ไม่มาก
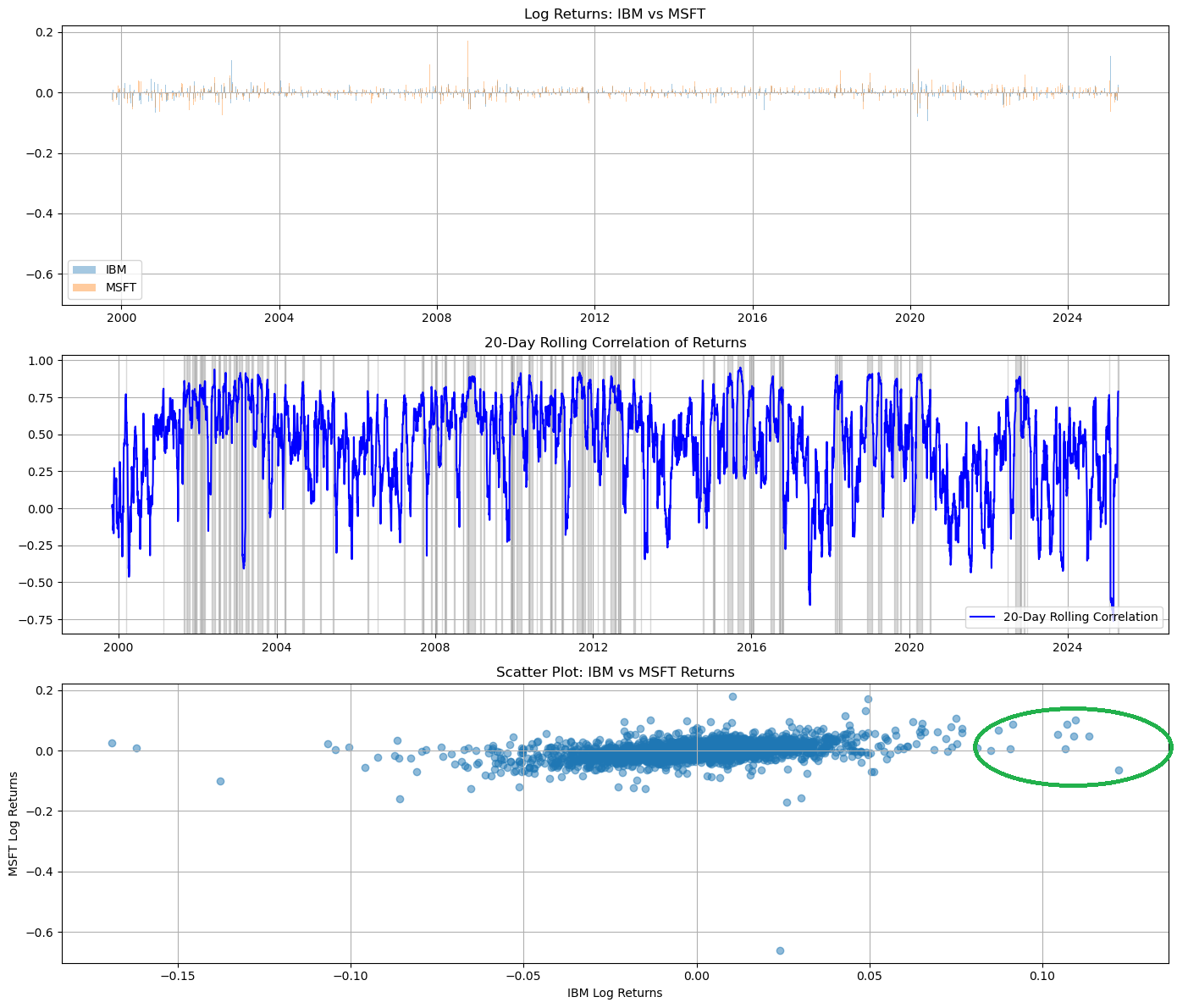
แต่หากพิจารณา ข้อมูลย้อนหลังตั้งแต่ปี 2000 (รูปที่ 2 Panel 3)
พบว่าแม้ correlation โดยรวมจะต่ำ แต่มี Upper Tail Dependence ที่สังเกตได้ชัด
👉 เวลาขึ้นแรงมักไปด้วยกัน แต่เวลาลงแรงอาจไม่ลงพร้อมกัน

🛠️ การประยุกต์ใช้ Tail Dependence

📊 การบริหารพอร์ตการลงทุน (Portfolio Risk Management)

ใช้เพื่อประเมินว่า สินทรัพย์ที่ดูแตกต่างกัน จะพังพร้อมกันในช่วงวิกฤตหรือไม่
ตัวอย่าง: หุ้นพลังงานและหุ้นเทคโนโลยี แม้ดูไม่สัมพันธ์กัน แต่เมื่อเกิด shock ระดับมหภาค เช่น COVID-19 หรือ Trump Tariff — ทั้งคู่ร่วงพร้อมกัน

🏦 การบริหารเงินทุนของสถาบันการเงิน (Capital Management)

Tail Dependence ถูกใช้ในการประเมิน Value-at-Risk (VaR) และ Expected Shortfall ให้แม่นยำขึ้น
โดยเฉพาะกับพอร์ตสินทรัพย์ที่มีพฤติกรรมร่วมที่ไม่เป็นเชิงเส้น

🧠 การคำนวณ Tail Dependence

Tail Dependence สามารถนิยามได้สองรูปแบบที่สำคัญ:

นิยามผ่าน Copula Function
นิยามผ่าน Conditional Probability (แบบ intuitive สำหรับการตีความ)

ทั้งสองแนวทางให้ความเข้าใจลึกซึ้งเกี่ยวกับ โครงสร้างความสัมพันธ์เชิงสุดขั้ว (extreme dependence structure) ระหว่างตัวแปรสุ่ม

🟥 1. Lower Tail Dependence (λ_L)

วัดความน่าจะเป็นที่ \( X \) และ \( Y \) จะ ลดลงอย่างรุนแรงพร้อมกัน

\[ \lambda_L = \lim_{u \to 0^+} \mathbb{P}\left( Y \leq F_Y^{-1}(u) \,\middle|\, X \leq F_X^{-1}(u) \right) \]

🔍 คำอธิบายตัวแปร:

สัญลักษณ์	ความหมาย
\( X, Y \)	ตัวแปรสุ่มสองตัว เช่น ผลตอบแทนของสินทรัพย์
\( F_X, F_Y \)	ฟังก์ชันสะสมความน่าจะเป็น (CDF) ของแต่ละตัวแปร
\( F_X^{-1}(u), F_Y^{-1}(u) \)	ค่าควอนไทล์ที่ระดับ \( u \) เช่น ค่าที่ต่ำกว่าร้อยละ \( u \) ของข้อมูล
\( u \to 0^+ \)	มองที่ค่าต่ำมาก (บริเวณหางซ้ายของการแจกแจง) เช่น \( u = 0.01 \) หรือ \( 0.001 \)

✨ ใช้เพื่อดูว่า

“ถ้า \( X \) ร่วงหนักมากๆ แล้ว \( Y \) จะมีแนวโน้มร่วงตามหรือไม่?”

🟩 2. Upper Tail Dependence (λ_U)

วัดความน่าจะเป็นที่ \( X \) และ \( Y \) จะ พุ่งขึ้นแรงพร้อมกัน

\[ \lambda_U = \lim_{u \to 1^-} \mathbb{P}\left( Y > F_Y^{-1}(u) \,\middle|\, X > F_X^{-1}(u) \right) \]

🔍 คำอธิบายตัวแปร:

สัญลักษณ์	ความหมาย
\( u \to 1^- \)	มองที่ค่าที่สูงมาก (บริเวณหางขวาของการแจกแจง) เช่น \( u = 0.99 \) หรือ \( 0.999 \)
ตัวแปรอื่น ๆ	เหมือนกับนิยามใน \( \lambda_L \)

✨ ใช้เพื่อดูว่า

“ถ้า \( X \) พุ่งขึ้นแรงมากๆ แล้ว \( Y \) จะพุ่งขึ้นตามหรือไม่?”

🔄 สรุปเปรียบเทียบสองนิยาม:

นิยาม	สูตร (แบบ Copula)	สูตร (แบบ Conditional Prob.)
Lower Tail (λ_L)	\( \lambda_L = \lim_{u \to 0^+} \frac{C(u,u)}{u} \)	\( \lambda_L = \lim_{u \to 0^+} \mathbb{P}(Y \leq F_Y^{-1}(u) \mid X \leq F_X^{-1}(u)) \)
Upper Tail (λ_U)	\( \lambda_U = \lim_{u \to 1^-} \frac{1 - 2u + C(u,u)}{1 - u} \)	\( \lambda_U = \lim_{u \to 1^-} \mathbb{P}(Y > F_Y^{-1}(u) \mid X > F_X^{-1}(u)) \)

📌 ทั้งสองนิยามให้ผลลัพธ์เทียบเคียงกันได้ในเชิงพฤติกรรม Tail Risk
แต่แบบที่สอง (Conditional Probability) ตีความง่ายกว่า และเหมาะกับการอธิบายเชิงประยุกต์ในเชิงพอร์ตและระบบการเงิน

🧠 การคำนวณ Tail Dependence จากข้อมูลจริง (Empirical Estimation)

Tail Dependence คือความสัมพันธ์ของตัวแปรสุ่มในช่วง “หางของการแจกแจง” เช่น เหตุการณ์สุดขั้วในตลาด
เราสามารถคำนวณจากข้อมูลจริงโดยไม่ต้องสมมติฟังก์ชันการแจกแจงล่วงหน้า ด้วยวิธี Empirical (Nonparametric)

✅ Input:

ข้อมูลผลตอบแทนรายวันของสินทรัพย์สองตัว เช่น หุ้น IBM และ MSFT
ข้อมูลควรจัดเรียงตามเวลา และมีจำนวนข้อมูลมากพอ (เช่น 500 จุดขึ้นไป)

🔢 Step-by-step:

🔹 Step 1: เตรียมข้อมูล

สร้างเวกเตอร์ผลตอบแทนรายวัน: \[ R_X = [r_{X,1}, \dots, r_{X,n}], \quad R_Y = [r_{Y,1}, \dots, r_{Y,n}] \]
ตรวจสอบให้ข้อมูลเรียงวันตรงกัน (time-aligned)

🔹 Step 2: แปลงข้อมูลเป็นค่าควอนไทล์ (Empirical Quantiles)

แปลงค่าผลตอบแทนเป็นตำแหน่งในข้อมูล (rank) แล้วหารด้วย \( n+1 \):

\[ U_i = \frac{\text{rank}(R_{X,i})}{n + 1}, \quad V_i = \frac{\text{rank}(R_{Y,i})}{n + 1} \]

ผลลัพธ์คือ \( U_i, V_i \in (0,1) \) อยู่ในรูปของ อันดับสัมพัทธ์ ของแต่ละจุดข้อมูล

🟥 Step 3: คำนวณ Lower Tail Dependence \( \hat{\lambda}_L(u) \)

เลือกค่า \( u \) ที่แสดงถึงหาง เช่น \( u = 0.05 \)

\[ \hat{\lambda}_L(u) = \frac{ \#\{ i : U_i \leq u \,\land\, V_i \leq u \} }{ \#\{ i : U_i \leq u \} } \]

หมายถึงความน่าจะเป็นที่ \( Y \) จะตกแรง เมื่อ \( X \) ตกแรงเช่นกัน

🟩 Step 4: คำนวณ Upper Tail Dependence \( \hat{\lambda}_U(u) \)

เลือกค่า \( u = 0.95 \) เพื่อดูพฤติกรรมด้านขวาของหาง

\[ \hat{\lambda}_U(u) = \frac{ \#\{ i : U_i > u \,\land\, V_i > u \} }{ \#\{ i : U_i > u \} } \]

หมายถึงความน่าจะเป็นที่ \( Y \) จะพุ่งแรง เมื่อ \( X \) พุ่งแรงเช่นกัน

🔍 คำอธิบายตัวแปร:

สัญลักษณ์	ความหมาย
\( U_i, V_i \)	ค่าควอนไทล์แบบ empirical ของ \( R_X \) และ \( R_Y \)
\( u \)	ค่าคัดกรองหาง เช่น 0.05 (5%) หรือ 0.01 (1%)
\( \#\{ \cdot \} \)	จำนวนข้อมูลที่เข้าเงื่อนไข

🖥️ ตัวอย่างโค้ด Python (Empirical Estimation)

import numpy as np
from scipy.stats import rankdata

def empirical_tail_dependence(x, y, u=0.05):
    n = len(x)
    ux = rankdata(x) / (n + 1)
    uy = rankdata(y) / (n + 1)

    lower = np.sum((ux <= u) & (uy <= u)) / np.sum(ux <= u)
    upper = np.sum((ux > 1 - u) & (uy > 1 - u)) / np.sum(ux > 1 - u)

    return lower, upper

ความเสี่ยงที่หาง (Tail Dependence)