A 1/t algorithm with the density of two states for estimating multidimensional integrals
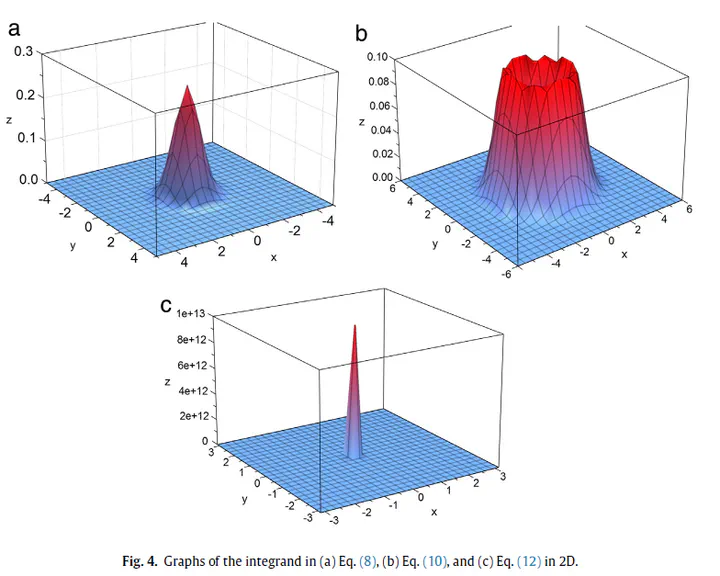 Image credit:
Image credit:Abstract
In this work we developed a 1/t algorithm for numerical integration in high dimensions. A large amount of computation time is wasted when a random walker is unable to reach a rare state at the sharp peak of an integrand, and becomes trapped after falling through that state. In this study, the density of states was divided into only two levels by sampling an arbitrary point in the range of the integrand, rather than into many levels using a fixed bin width (grid discretization on continuous space). The technique is quite straightforward and easy to implement. It avoids the need to determine the exact boundaries of the integrand, which is often a non-trivial task. Simulations show that our method is able to significantly reduce the number of Monte Carlo trials required, and therefore the simulation time. The potential of the proposed method was demonstrated by application to two multidimensional integrals, the Gaussian ring and the setting sun Feynman diagram. The results confirm that the proposed method can be applied to the calculation of multidimensional integrals without error saturation, yielding accurate values in applications where other numerical methods fail.
Type
Publication
Computer Physics Communications, 220, 122-128, 2017